Console-Pathfinding
Daniel Bortfeld - Code Snippet: BreadthFirst, BestFirst, Dijkstra and A* on a Grid in the Console
Project maintained by DanielBortfeld Hosted on GitHub Pages — Theme by mattgraham
Pathfinding demonstrated in the Console
Content
A*
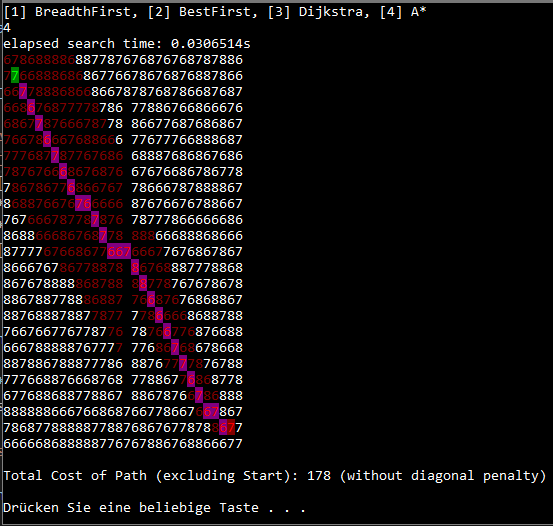
This console application demonstrates the pathfinding algorithms BreadthFirst, BestFirst, Dijkstra and A*. The picture below shows the result for a path searched with A*. The green point represents the start of the path, the red point is the goal. The path itself is colored pink/purple. Dark red numbers have been taken from the open list and have been investigated for a path. White numbers have not been investigated. The numbers represent both the nodes and the cost of traversing the node. Black points can not be traversed.
Code
Prerequisites
In order to perform the pathfinding algorithm some prerequisites are necessary. First, you need a graph with interconnected nodes. The nodes can be connected via edges. In my case I chose not to use edges but to consider all neighboring nodes to be connected with the node I’m currently looking at.
Furthermore, I’m using a priority queue as the open list.
Nodes
The Nodes contain information about their position and coloration in the grid, whether they are walkable and how much it costs to walk on them. During the A* algorithm further information is needed about the parent node, the real, heuristic and estimated cost, whether the node is on the open list and what the open list should sort the node by.
// Node.h
//...
enum SortBy
{
RealCost,
Heuristic,
Estimate
};
class Node
{
public:
int X;
int Y;
bool IsWalkable;
int Cost;
char Color = Color::IntenseWhite;
Node* Parent;
float RealCost;
float Heuristic;
inline float EstimateCost() const { return RealCost + Heuristic * HeuristicWeight; }
float HeuristicWeight = 1.0f;
bool IsOnOpen = false;
SortBy SortType = SortBy::Estimate;
// ...
The priority queue (open list) will sort the nodes inside it using the greater > operator so that the node with the lowest cost will end up at the front/top of the list.
// Node.cpp
bool Node::operator>(Node const & other) const
{
switch (SortType)
{
case SortBy::RealCost:
return RealCost > other.RealCost;
case SortBy::Heuristic:
return Heuristic > other.Heuristic;
case SortBy::Estimate:
return EstimateCost() > other.EstimateCost();
default:
return Cost > other.Cost;
}
}
Priority Queue
I’m using the std::priority_queue with two additions for my pathfinding. Because you cannot find and remove elements in/from the std::priority_queue, I have added two functions to facilitate this functionality for the purpose of pathfinding.
// PriorityQ.h
//...
class PriorityQ : public std::priority_queue<Node, std::vector<Node>, std::greater<Node>>
{
public:
auto Find(Node* node);
void Reinsert(Node* node); // remove the 'node' from the queue and push it back in in order to resort the queue
};
A*-Algorithm
This is my A* algorithm with comments explaining it step-by-step.
// Pathfinder.cpp
// the graph was prefilled and forwarded from the main(). the start and goal node are part of the graph.
bool Pathfinder::AStar(std::vector<std::vector<Node*>>& graph, Node * start, Node * goal)
{
// the open list holds the nodes that have not been investigated by the algorithm
PriorityQ openList;
// the closed list holds the investigated nodes
std::vector<Node*> closedList;
// the start node initially gets pushed on the open list to be the first investigated node.
// you could also start with the goal and look for the start, but I'm searching from start to goal
openList.push(*start);
// the search continues as long as there are uninvestigated nodes
while (!openList.empty())
{
// the PriorityQ holds objects instead of pointers because the comparison function of the std::priority_queue
// can not compare the objects behind pointers. instead it would compare the memory adresses itself.
// to make sure the node from the open list is the same as the one in the graph, the corresponding pointer is
// taken from the graph. popped nodes become colored red and pushed onto the closed list.
Node temp = openList.top();
Node* current = graph[temp.X][temp.Y];
openList.pop();
current->Color = Color::Red;
current->IsOnOpen = false;
closedList.push_back(current);
if (current == goal)
{
// the path gets traced back through the parent connections untill we reach the start
while (current != nullptr && current != start)
{
// nodes belonging to the path become colored red/pink
current->Color = Color::IntenseRed + Color::PinkBackground;
TotalPathCost += current->Cost;
current = current->Parent;
}
return true;
}
// if the goal has not been reached yet
// all neighboring nodes of the current node are gathered for further investigation
for (int x = -1; x < 2; x++)
{
for (int y = -1; y < 2; y++)
{
// don't consider yourself as a neighbor
if (x == 0 && y == 0)
{
continue;
}
int X = current->X + x;
int Y = current->Y + y;
// make sure the index is still in range
if (X < 0 || X > graph.size() - 1 || Y < 0 || Y > graph[0].size() - 1)
{
continue;
}
// the node you can reach from the current node (from = current, to = neighbor)
Node* toNode = graph[X][Y];
// don't consider unwalkable nodes and also
// don't consider nodes that have been investigated already and ended up on the closed list
if (!toNode->IsWalkable || std::find(closedList.begin(), closedList.end(), toNode) != closedList.end())
{
continue;
}
// calculate the actual cost for getting from the start to this node
// and the heuristic cost for getting from this node to the goal
float realCost = current->RealCost + ((current->X == toNode->X || current->Y == toNode->Y) ? toNode->Cost : toNode->Cost + 0.4f); // with diagonal penalty
//float realCost = current->RealCost + toNode->Cost; // without diagonal penalty
float heuristic = sqrtf(abs((goal->X - toNode->X)*(goal->X - toNode->X) + (goal->Y - toNode->Y)*(goal->Y - toNode->Y))); // euclidean
//float heuristic = (goal->X - toNode->X) + (goal->Y - toNode->Y); //manhattan
// if the node is already on the open list
if (toNode->IsOnOpen)
{
// and if the cost is smaller than last time we checked
if (realCost < toNode->RealCost)
{
// update the node with the new infos
toNode->RealCost = realCost;
toNode->Heuristic = heuristic;
toNode->Parent = current;
openList.Reinsert(toNode); // resorts the priority queue
}
continue;
}
// the node has not been touched before, so it gets filled with information
toNode->Parent = current;
toNode->IsOnOpen = true;
toNode->RealCost = realCost;
toNode->Heuristic = heuristic;
// the sort type is set to estimate because this is what it's sorted by when using A*
toNode->SortType = SortBy::Estimate;
// the heuristic weight gives a higher or lower value to the heuristic cost.
// a weight of 4.5 allows better results than a weight of 1, if we are using
// the currently randomly filled graph/map
toNode->HeuristicWeight = 4.5f
// the node gets pushed to the open list for further investigations checking whether it's the goal
// or has any neighbors that might be the goal.
// this also resorts the priority queue
openList.push(*toNode);
}
}
}
// there is no path
return false;
}
Further pages: